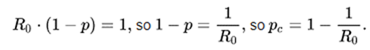|
Data Police episode
540: The herd and the immunity. |
|
|
|
|
|
|
|
|
last update 20200515 |
|
|
This is a component
of the ad hoc covid19 data project connected to the FUFF platform (fuff.org) |
|
|
http://fuff.org/data/cr0.html |
|
|
It includes a link to
the model used below for the calculations |
|
|
|
|
| 1 |
One concept that is
currently being discussed scientifically and not so scientifically is the
concept of community immunity, often referred to as 'herd immunity'. |
|
|
|
|
| 2 |
I will only focus
here on the very basic mathematical idea. Like the one you will find in the
following Wikipedia article I will not go into how immunity is achieved and
whether it is acceptable. |
|
|
https://en.wikipedia.org/wiki/Herd_immunity |
|
|
|
|
| 3 |
However, I must at
least mention some contextual aspects, as they are heavily interfering with
all those mathematical concepts. |
|
|
|
|
| 4 |
For example: Immunity
might not be a truely binary state.
Or: Immunity might not be indefinite and this could mean that a wide range
of length (time) of immunity is possible
(All this has not yet been researched for this virus). |
|
|
|
|
| 5 |
And: All this will be
different to some degree in different human beings and possibly for different
mutation strains of the virus as well. |
|
|
|
|
| 6 |
That means that in a
not so simplified model calculation we are dealing with a lot of probability
distributions. This in turn means we might speak of broad and flat confidence
intervals (a very fuzzy result). And we might be carrying a high risk outside
the confidence interval. There is a huge difference in risk if you have a
gradually worse situation outside your confidence interval or a collapsing
situation. |
|
|
|
|
| 7 |
Also, I should at
least mention that a part of the immunity may be represented in fatalities.
While this does not affect an oversimplified abstract model (depends on the
construction as well), it will make a difference in the real world because
there will be some compensation for lost contacts (simple example: a
hairdresser). |
|
|
|
|
| 8 |
So what I will look
at here is the mathematical concept I see in the public discussion: The very
simplified idea of a homogenous 'herd' containing so many infected members
that the reproduction rate sinks below 1 and reproduction fades out, because
the infected member does not meet enough contacts that are still uninfected
to further spread the virus. |
|
|
|
|
| 9 |
The first thing that
springs to mind is that the metaphor ('herd') does more bad than good. Like
all metaphors it highlights and hides different properties of the
metaphorized. But it does not mean equality.
A human population is no 'herd'. |
|
|
|
|
| 10 |
When 'herds' are
spoken of in the covid19 context it usually refers to the population of a
country, or more precisely: to all people that are currently present in a
geographical zone. |
|
|
|
|
| 11 |
But those people are
not a hegemonic group of equals crammed together in a stable, while still
freely moving around inside and randomly meeting each other. |
|
|
|
|
| 12 |
We are talking of a
population consisting of regional clusters, organised in hub structures, with
permeable borders between them. |
|
|
|
|
| 13 |
And then we are also
talking of a population consisting of behavioural clusters, with gradually
different behaviour within themselves, and again with permeable cluster
boundaries. (the clusterization is a crutch) |
|
|
|
|
| 14 |
Those two facts alone
ridicule any thumb rule for calculatiing 'herd immunity' from a R0.
Like the ones you find on the internet.
For example in the above mentioned Wikipedia article.
They are darts thrown at an imagined board hanging somewhere in the
darkness. |
|
|
|
|
|
|
|
| 15 |
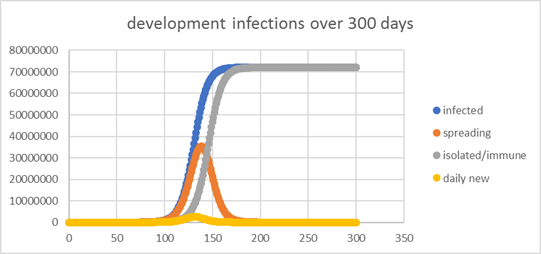
The very first
component that is neglected here is time. That was a serious threat when the
pandemic began.
If you have a system where infection spreads from zero exponentially and
the ratio of time needed for immunization to time needed for the exponential
reproduction is the same as in the case of covid19, your immunity rate will
remain pure theory. Before the necessary immunity level is reached, already
90% are infected. However that is just mathematics, and the calculation model
is nearly as simplified as the common immunity calculation formula I just
attacked. Like that formula, it does not take into account behavioural
change, interventions etc.. And like that formula our population consists of
a real 'herd', randomly meeting each other regardless of distance, all
behaving the same, etc.. |
|
|
|
|
|
example is for a
population of 80 million, R0=Rt=2.5, time to immunity 15 days |
|
|
|
|
| 16 |
Now what if we assume
that 50-60% are already immune and that the virus starts from scratch and
that our population is a 'herd' like a cow herd or a sheep herd?
Here is what our simplifed distribution model spits out now: |
|
|
|
|
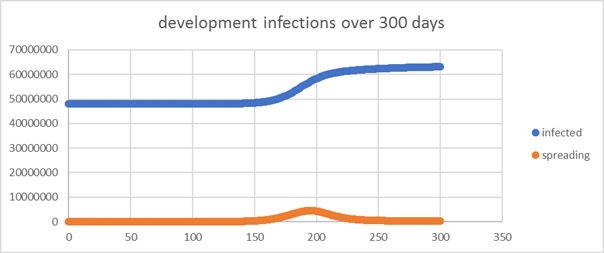
|
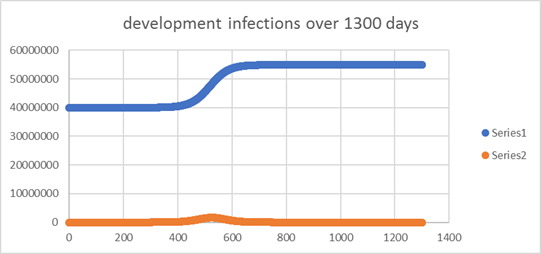
At 50% (left chart)
there is still a considerable crisis with close to 15 million new infections,
at 60% (right chart) this dries down to only a few hundred |
|
|
You might think it is
a contradiction, that a system that enters with 40 million infections
produces a higher total than one that enters with 48 million.
It is not. A system without interventions would not have stopped at 50
million in the first place. See the example above. |
|
|
|
|
| 17 |
So 60% is enough to
stop further spread of infections in our HERD (60% immune, virus starting
from scratch = 1 infection).
BUT ONLY if the outcome is average(!), ONLY if the group is homogenous,
ONLY if mixing perfectly and randomly even of infected and non-infected
(regardless of distance between them). And all behave the same (have the same
job, travel the same, meet the same number of people, speak the same amount
etc etc.).
So: Only in a scenario that is NEVER the case. |
|
|
(In the same time the
resulting outcome is very sensitive to the frame parameters, such as the
number of days until immunity/isolation, the actual R0). |
|
|
|
|
| 18 |
In reality now you
will - instead - have clusters (or clumps) of uninfected persons, of which
not all will have reached that necessary level of community immunity. Think
of regional differences, think of (not so perfectly) sealed off groupings
like nurse homes. |
|
|
|
|
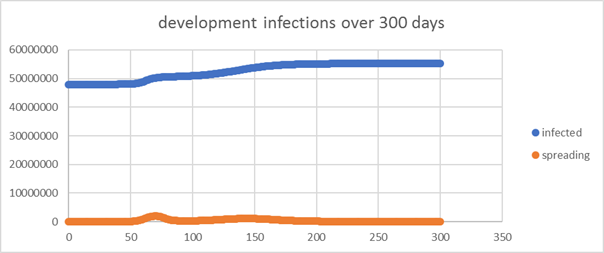
| 19 |
Now we change the
scenery: let's use a cluster model with an initial 60% immunity level
overall, but that immunity is unevenly distributed across the clusters. |
|
|
|
|
|
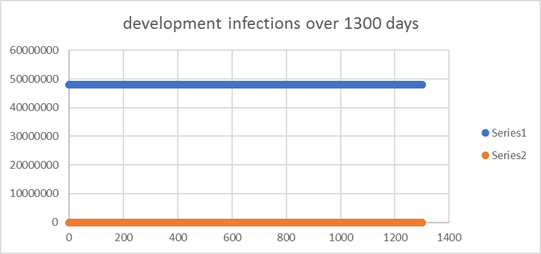
With a simple model
of 4 equal sized clusters with 86%, 80%, 54%, and 20% immunity, we get a
veritable crisis again within a few hundred days from 1 infection. More than
15 million additional infections instead of a few hundred, simply because the
uneven distribution of the 60% immunity. |
|
|
|
|
| 20 |
This seems to
completely destroy any idea of a realistic immunity level below 90%.
BUT not so fast - the matter is complex (in fact it is even much more
complex than I make it here). |
|
|
|
|
| 21 |
The fact that we do
not have a homogenous herd with an even distribution of contacts, can
actually work in our favour, too. However you have to remember that this is
not a linear process even we end up here with values that suggest this. |
|
|
|
|
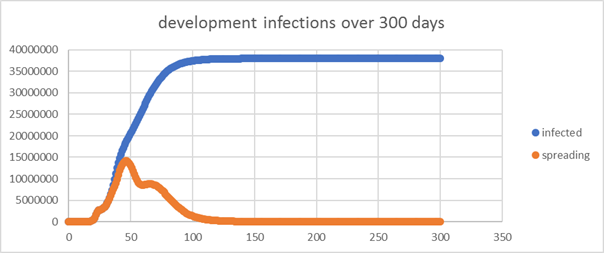
| 22 |
If now we add a
behavioural cluster layer to the above example, in which we assume that it is
more likely that a more active cluster is also more likely to have already
reached a higher immunity level (not necessarily the case, so I mixed it a
bit), the whole thing looks a bit more friendly. |
|
|
|
|
|
Again, change of
parameters have big effects, and eventually, more and more details are
guessed at during the design process. |
|
|
|
|
| 23 |
To fully understand
the immunity concept let us recap something:
The 60% 50% 80%, whatever, they are immune.
The remaining 40% 50% or 20% however, they are not immune at all. Not one
bit. |
|
|
|
|
| 24 |
With a 'community
immunity' we simply do not expect the average infection case to cause an
epidemic, because we assume the Rt to stay below 1. |
|
|
|
|
| 25 |
But Rs are just
averages of distributions and those distributions are asymmetrical and can
have very long (or 'fat') tails, that may come into effect as a surprise.
Think of the 'superspreaders' (an individual reproduction rate that lies far
outside the expected spectrum). Calculated Rs can be deceptive, as there is
always a value possible for the future that is far further outside the
spectrum than anything you have had until now. |
|
|
|
|
| 26 |
Nor are countries
sealed off zones, and no country plans to never open its borders again or
would be able to make them impermeable. |
|
|
|
|
| 27 |
All this I do not
find in the formulas proposed on the Internet, although I am confident they
are accounted for in real experts models. |
|
|
|
|
| 28 |
So the proposed
immunity levels are not very solid.
But that does not necessarily mean doom and gloom: Indeed we can have very
positive effects by combining the reduction of Rt through behavioral change
and the slowing of multiplication through partial immunity. It is just very
complicated and is likely to be of greater benefit to certain
clusters..
And slow does not mean the virus is less dangerous for the individual or
less likely to mutate. |
|
|
|
|
|
Here we have chosen
the cluster parameters in such a way that the epidemic comes to a halt even
before the infection level reaches 50%. Without intervention. But it is
absolutely forbidden to take results like this as a serious calculation with
all the guessing of parameters involved and ignorance of the parameters not
involved |
|
|
|
|
| 29 |
If you play around
with our simple model, the redefinition of the included variables alone
suggests such a dynamic change in the scenario that predicting the required
level of immunity is very fragile and fuzzy. And the answer must be complex,
taking into account all the above aspects. |
|
|
|
|
| 30 |
Here we see many
politicians embracing simple answers, preferring rules of thumb and traffic
light variables to facilitate their political choices and offer apparent ways
out of real dilemmas, which however do not disappear by being ignored.
They do not seem up to the task of challenging such a complex problem and
manouver through a complex world. But even this is not proven, I guess. |
|
|
|
|
|
|
|
|
Do you have anything
to correct? add? |
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|