this is an example result from the experimental simulation model you find under the adress

the miracle of math(sk)s

This is a simplified model - however, I want to show a mathematical effect at an uncomplicated example.

It is not about the precise numbers.

Imagine a population where each already infected person has a probability of infecting 1.3 others within the following 15 days.

We start with 1 infected person

Here is what happens in this model:

one cluster, all persons are average persons

population:

80,000,000

devide:

100

depth:

days:

spread:

1.3

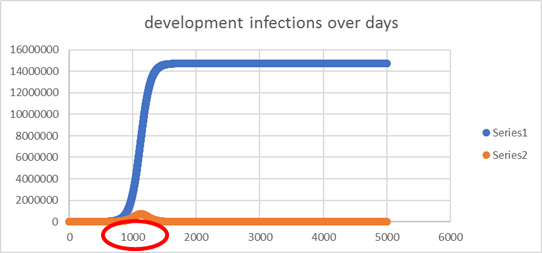
It will take some time, 1.3 is not much, for example because some social(physical) distancing is in place. So in the average case, after 300 days the wave will finally come and 35 million will become infected within roughly 200 days

Now, imagine, the people all wear masks. Masks that maybe are not perfect, but in our example they reduce that spread potential by 15% (only 15%!). So it is now 1.105

Does not seem much, eh?

Now see what happens

one cluster, all persons are average persons

population:

80,000,000

devide:

100

depth:

days:

spread:

1.105

we even have to revert to a wider

time scale to see the full result:

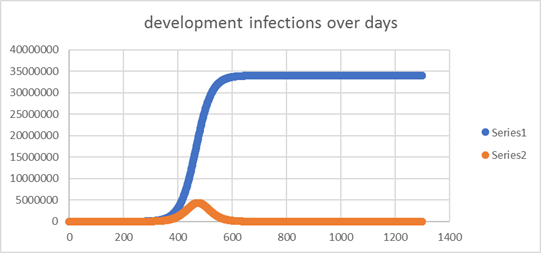
Two effects: It takes almost double the time and the spread is exhausted at below 15 million infections.

That is not 15% less. It is more than 57% less!

The effect is even more stunning when exercised close to the tipping point of 1.

Let's assume the above mentioned 1.105 scenario is the one without the masks.

Now we are reducing that by 15% through the masks:

one cluster, all persons are average persons

population:

80,000,000

devide:

100

depth:

days:

spread:

0.93925

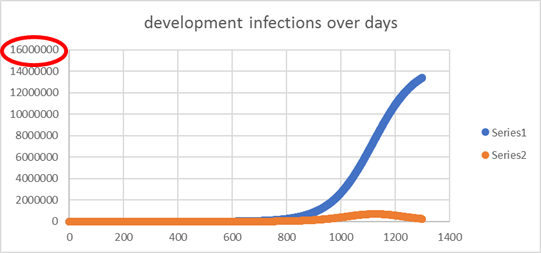
Well, the whole thing dies out sooner or later - at an average of 16 infected people

That is not 15% less. That is almost 100% less.

How that?

Spreading the virus is a generational model opf multiplications. One person spread it to x persons, and those will spread it again to x persons each. And so on.

So every influence on the spread multiplies in the following generations and multipies again and so on.

Think of the easy example of 4 generations and a virus that each person spreads to 4 others.

the first person spreads to 4, those to 4 each, which makes it 16, and those to 4 each, what is 64.

After 4 generations you have 1+4+16+64=85 infected

Now this is reduced by 25% through some kind of behavioural change, lockdown, masks, whatever.

now the first person spreads to 3, those to 3 each, which makes it 9, and those to 3 each, what is 27.

After 4 generations you now have 'only' 1+3+9+27=40 infected.

Which is not 25% less but more than 50% less.

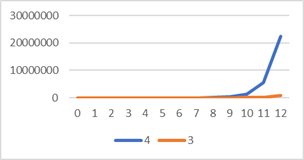
After 12 'generations' you have a whopping effect:

341

1365

5461

21845

87381

349525

1398101

5592405

22369621

121

364

1093

3280

9841

29524

88573

265720

797161

800 thousand vs. 22 million. The reduced curve is still exponential but that is a different quality.

-> Disclaimer: In complexer reality the extent of this effect would depend very much on the potential, the size of the country, overlapping of clusters etc. This is not accounted for in this example, but it is in the models at the top of this page.

This huge 'success' comes because the effect multiplies itself with each generation.

From the first to the second generation it is indeed 25% less - or: 0.75 times the original value.

But from first to third generation it is now 0.75*0.75 of the original spread, which is 0.5625. And from the first to the fourth it is 0.75*0.75*0.75 (=0.4219)

And so on.

So over time this effect can become huge.

However, in our model a step down from 4 to 3 in spread does only help a little.

It gives us more time, but the eventual outcome will still be a quite rapid infection of almost the whole population. A few millions will be saved from it, though.

So, just wearing masks alone would be no solution.

But wearing masks in the right context could have a huge effect as shown above.

Even if a clustered model (closer to reality) will soften the effect a bit.

experiment yourself…

http://fuff.org/data/cr0.html

*DISCLAIMER

again: this is a simplified model to show some mathematical effects and properties and inspire collaboration and your efforts. It is not a proper simulation to base decisions upon.