This is a component of the ad hoc covid19 data project connected to the FUFF platform (fuff.org)

this is an example result from the experimental simulation model you find under the adress

the dangers of averages

everybody knows that 2*6 <> 4*4 although 4 is the average of 2 and 6. But as apparent as that is, related misconceptions hide everywhere where you might happily apply seemingly simple probabilities and probability chains.

in the following I try to show for a very simple probability based infection model, how clusterization can flip a whole scenario on its head (because of the aforementioned properties of the application of averages).

disclaimer: this model is a grossly simplified abstract to demonstrate mathematical properties and dangers in applying 'right' mathematics in the wrong context - don't use it to jump on conclusions for real scenarios!

but even with this simple approach I can demonstrate to you what terrible difference wrong application of averages, aggregations and values can do

(- and why I implemented a clustered model at least):

think of a simulation where the spread/person (a value closely related to the famous R0) is only 0.8 over the whole population

it means that each infected person in the model would spread a virus to 0.8 others (here over a strech of being infectous for 15 days before becoming muted):

beginning with 1 infected perosn, now here is what happens:

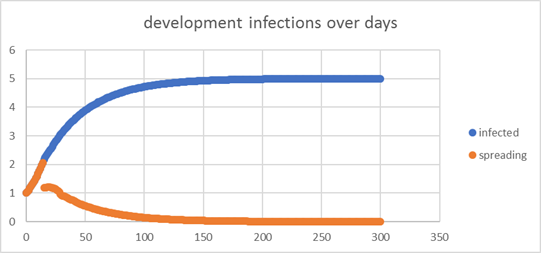
one cluster, all persons are average persons

population:

80,000,000

devide:

100

depth:

days:

In average 5(!) people would be infected after 300 days

-> now that is an average(!), too. In reality it is a distribution and it could be 0, or could be several hundred. It is a set of probabilities centering around the 5, not a concrete result!

However, the point I want to show here is the following:

below is what happens if the persons in the model have a spread probability of 0.8 in average

but individually they would have different spread probabilities, one had 1.5, one 0.5, one 0.4 etc.

In this model this is simulated by clusters of higher and lower spread/person averages.

Why? -> We would assume that there are behavioural and/or geographical clusters rather than an evenly distributed population/behaviour.

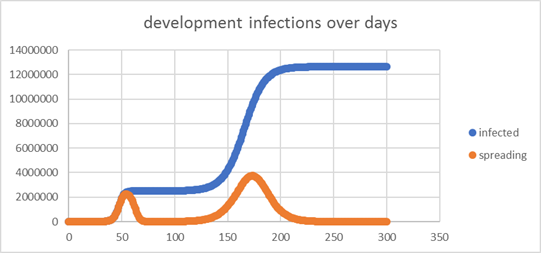
I choose the values a bit extreme to get the idea across

32 clusters with differend spread probabilities, but overall all persons will spread to others 0.8 in average

population:

80,000,000

devide:

depth:

days:

after 300 days we are at 12,000,000 as some clusters explode while others remain muted

12,000,000 vs. 5 (just 5, not 5 millions) - that is something different

-> this simplified approach does not take into account leakage of spread from one cluster to another. this would modify the result a little but not in principle.

-> do not mistake this value for the R0 value you would calculate in retrospective. In retrospective of course you would calculate a different R0 than the spread probability for each person we went into this simulation here. But this is not the point.

let's explain the effect at a simple example:

imagine 2 person groups with an average R of 1.

If both infection chains spread equally with an R=1, in the 4th generation you get

1+1*1+1*1*1+1*1*1*1 = 4 infected persons * 2 persons = 8 infected persons

now think of one group/chain spreading to 1.5 persons in average, the other spreading to 0.5 persons in average, if they become infected.

overall you go into that calculation again with an average R of 1

but the result willl be different:

1+1*1.5+1*1.5*1.5+1*1.5*1.5*1.5 = 8.125 infected persons for one cluster

1+1*0.5+1*0.5*0.5+1*0.5*0.5*0.5 = 1.875 infected persons for the second cluster cluster

= 10 infected persons in total

naturally the retrospective calculation of an R value would give different resulting values for R, depending on the method this even changes over generations.

the reason is that in the calculation only the persons are considered that are actually spreading, and the cluster that is more active grows in the number of persons faster.

this is just an abstract model which is not much closer to reality than others. But it could show you how the wrong fit of details can completely flip a scenario.

Especially if you build on averages and aggregations of disparities.

And we do a lot here: even a countries official numbers are averages/aggregations of hot spot clusters and low crisis clusters with high potentials etc.

please review!